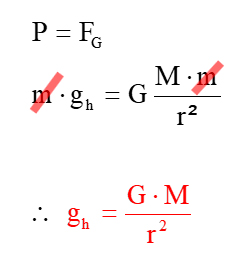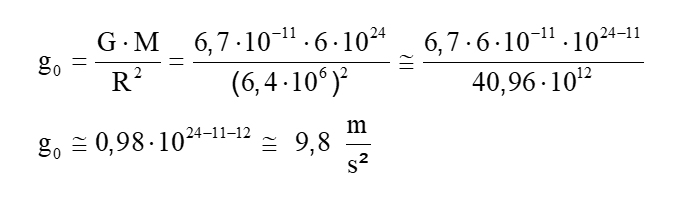Em postagem anterior, em que calculo a velocidade orbital da ISS – Estação Espacial Internacional, comentou o internauta “A gravidade da ISS em relação à Terra está errada.“
Foi estranho para mim, porque em nenhum momento calculei ou usei o valor da gravidade (ou campo gravitacional g) na ISS. O que fiz foi equalizar a força da atração gravitacional entre a Terra e a estação espacial para, a partir da idéia da força centrípeta resultante, descobrir com que rapidez a ISS ou qualquer outra espaçonave ou mesmo satélite, independentemente de sua massa, teria que orbitar ao redor Países a cerca de 400 km acima do nível do mar. E alcançamos um valor de quase 28.000 km / h, em alta velocidade pelos padrões humanos.
Mas o comentário foi legal, porque me fez querer fazer esse cálculo no post, algo que eu já havia feito na Física, mas em uma antiga plataforma de blog que era tecnicamente obsoleta e é por isso que o UOL o aboliu. É um bom momento para recuperar a idéia “perdida” no texto, que acabou no ar devido ao destino tecnológico!
Eu farei isso hoje. Mostrarei como calcular a gravidade (a rigor, o módulo do campo gravitacional) em torno de qualquer estrela. Usando a expressão que vou descobrir, podemos calcular quanto vale a gravidade na ISS, 400 km acima do nível do mar. Você verá que o fato de os astronautas estarem “flutuando” dentro da estação espacial, como no curioso vídeo acima do qual Chris Hadfield escova os dentes na estação espacial, nada tem a ver com “gravidade zero”. Aqui, a gravidade está longe de zero!
Venha comigo?
Campo gravitacional
Dizemos que ao redor de qualquer corpo com massa M, outro corpo também com massa m sofrerá uma força gravitacional FSENHOR desde o primeiro¹. E essa força é dada pela Lei da Gravidade Universal de Isaac Newton (1643-1727) publicada abaixo.
Em física, tecnicamente falando, dizemos que em torno de um corpo de massa M existe um campo de forças gravitacionais g gerado por M e, portanto, não depende de M. Esse campo permeia todo o espaço ao redor de um corpo de massa M. Mesmo quando m não está lá, o campo está presente devido a a massa M que a cria. Assim, uma vez dentro desse campo, qualquer outro corpo de massa m atrairá gravitacionalmente M. A figura abaixo ilustra essa idéia. Observe que M e m não precisam estar em contato físico para que a atração ocorra. Sempre que temos forças agindo à distância, sem contato, pensamos fisicamente em um campo de força.
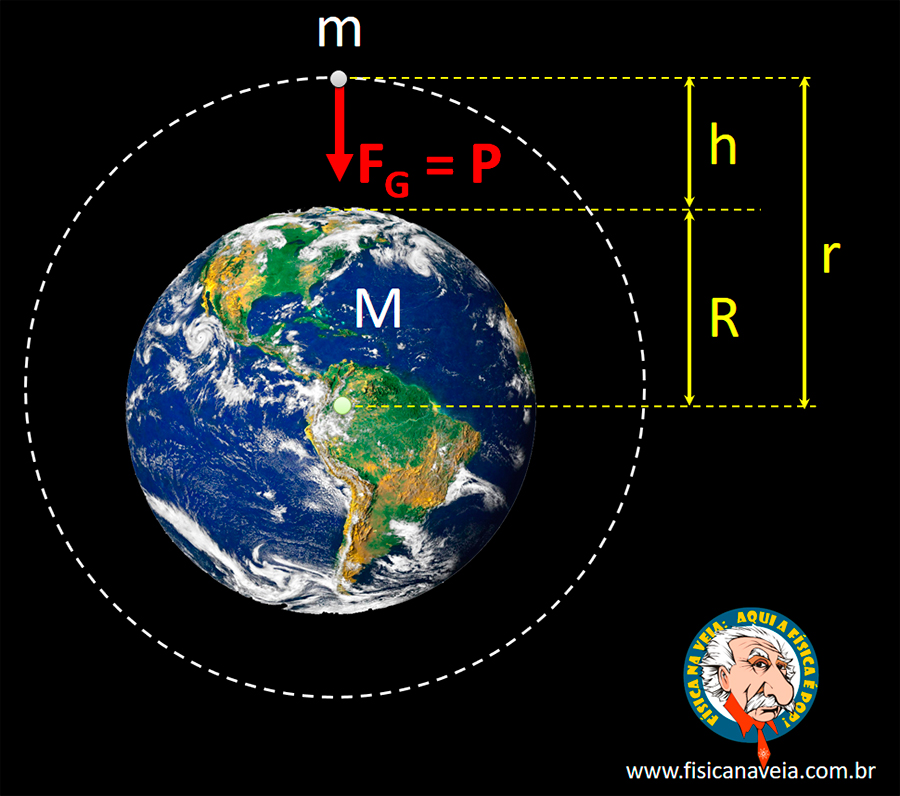
Uma terra (ou qualquer estrela esférica) de massa M atrai outro corpo de massa m que está à distância r = R + h. Um corpo de massa m pode ser a ISS ou qualquer outro objeto que orbita nosso planeta, incluindo um satélite artificial ou a Lua, nosso satélite natural.
Força gravitacional FSENHOR pode ser chamado de força do peso P. Abaixo você pode ver a definição da força do peso.
Como FSENHOR e P representam a mesma força de atração gravitacional, apenas escrita de maneiras diferentes nas expressões acima, podemos equipará-las. E na expressão que obtemos, podemos isolar o módulo de | g de acordo com outras quantidades físicas relevantes para o problema. Dessa forma, teremos uma “fórmula” pronta para calcular o módulo do campo gravitacional da estrela, que chamarei simplesmente de gravidade e, didaticamente, a partir de agora representarei SenhorH já que pensamos no valor de g em qualquer ponto ao redor de M e na altitude h. Veja:
Observe que, sem muito esforço, derivamos uma “fórmula” (expressão estritamente matemática) para calcular a gravidade em altitude ha da superfície da Terra ou de qualquer estrela ou, se preferir, a uma distância r = R + h do centro do campo esférico ou da Terra uma estrela de raio R. Na prática, uma estrela de massa M que cria um campo gravitacional nem precisa ser esférica se pensarmos que na expressão do campo gravitacional a distância r é medida do centro de massa do corpo M ao centro de massa do corpo m. , a expressão acima pode ser substituída alternando r para R + h. Confira abaixo.
Na superfície da Terra ou em qualquer estrela, para altitude h = 0, que na Terra podemos chamar de nível do mar, teremos r = R + 0 = R. E encontraremos outra expressão que nos dará a gravidade da Terra ou qualquer outra estrela, física um tamanho que chamarei de agora em diante Senhor0 0 porque h = 0. Verifique a expressão específica do campo gravitacional da superfície, ou seja, para h = 0.
Usando uma expressão Senhor0 0 acima, sabendo que a massa da Terra mede aproximadamente M = 6,1024 kg, cujo raio aproximado também vale R = 6400 km = 6,4.103 km = 6.4.106 m e que a constante gravitacional aproximada mede G = 6.710-11 kg.m² / kg², sem muito esforço, podemos obter o valor da gravidade da superfície Senhor0 0 a partir do solo:
E como não poderia ter sido de outra forma, descobrimos o valor tão esperado Senhor0 0 = 9,8 m / s² para a gravidade na superfície do nosso planeta, um valor ao qual estamos acostumados e para simplificação, frequentemente nos aproximamos de 10 m / s².
DICA IMPORTANTE: com expressão Senhor0 0 obtido e usado acima, você pode encontrar o valor da gravidade da superfície em qualquer planeta ou estrela. Basta pesquisar (por exemplo, Google) o valor do raio R e a massa M do objeto. Uma constante gravitacional universal G que você sempre pode usar G = 6.710-11 kg.m² / kg². E basta substituir na expressão g0 0 e olhe! Tente! Marte, Júpiter, a Lua, são alguns exemplos de estrelas cuja gravidade superficial você pode estimar.
Agora só temos que calcular o valor SenhorH para altitude h = 400 km, altitude aproximada da ISS e cumprir a missão do post de hoje. Teremos o valor da gravidade gerada pela Terra no espaço, 400 km acima da superfície, onde fica a estação espacial. Usaremos o termo para isso SenhorH obteve um pouco acima para a distância ISS da Terra de centro para centro, usando r = R + h = 6400 km + 400 km = 6800 km = 6.8103 km = 6.8.106 m. Veja o cálculo abaixo:
Descobrimos que a gravidade da Terra está nas medições da ISS SenhorH = 8,7 m / s², ou seja, longe de zero. Acima de 100 km, já podemos considerá-lo espaço. Portanto, há gravidade no espaço e na ISS! Essa gravidade zero no espaço é o maior roubo científico!
Observe que a expressão SenhorH obtido, seu valor diminui com o quadrado da distância até o centro da estrela. Em outras palavras, é inversamente proporcional a r². Portanto, se você se afastar da estrela e dobrar sua distância, a gravidade da estrela se enfraquece e cai para 1 / 2² = 1/4. Se a distância do centro da estrela triplicar, a gravidade se torna ainda menor e cai para 1/3 ² = 1/9. Se você quadruplicar essa distância, a gravidade diminui ainda mais e diminui para 1 / 4² = 1/16. E assim por diante. Você entendeu?
Estritamente falando, o campo gravitacional ou a gravidade de qualquer estrela será nulo e nulo somente se a distância r à estrela central estiver na direção do infinito. Então r² tenderá ao infinito, e dividiremos o GM pelo infinito, que chega a zero. É claro que após uma certa distância r o campo gravitacional será tão fraco que sua detecção será muito complexa. Podemos até dizer que, neste caso, é insignificante e, portanto, aproximação zero. Mas, estritamente falando, o campo gravitacional é realmente nulo e vazio apenas a uma distância infinita do corpo que o cria.
Por que os astronautas “flutuam” na ISS se a gravidade no espaço não é igual a zero?

Os astronautas Chris Cassidy e Andrew Morgan estavam “sentados” no ar e “flutuando” na ISS durante uma operação de manutenção. (crédito: NASA)
Se estivermos em um elevador e o cabo romper, o que, espero, nunca aconteça conosco, durante a queda do carro do elevador, teremos a sensação de que não temos peso, porque nosso corpo e o elevador cairão com a mesma aceleração a = Senhor0 0 = 9,8 m / s², um valor típico aqui na Terra e calculado acima. Se, por exemplo, você segurar um objeto e jogá-lo em um elevador em queda, ele (o objeto) ainda cairá com a mesma aceleração de 9,8 m / s². Para você, o objeto irá parar e “flutuar” na sua frente, mesmo que caia junto com você e o elevador, e todos “obtenham” uma velocidade de 9,8 m / s, ou 9,8 m / s cada.
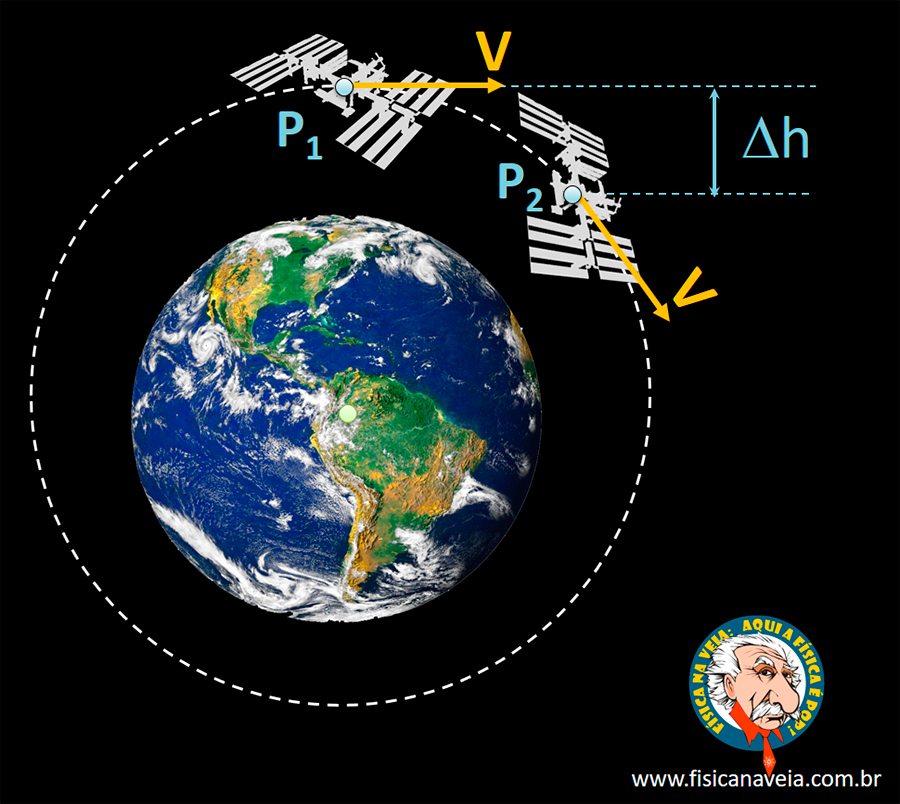
Na ISS, é praticamente a mesma coisa, porque a órbita não passa de uma queda infinita. Eu não entendi? Eu explico. Observe a ilustração abaixo, onde podemos ver (intencionalmente fora de escala) a ISS orbitando a Terra.
Imagine que, enquanto a ISS orbita a Terra, entre duas posições consecutivas P1 1 e P2 sempre cai uma quantidade de hh, mas segue a curvatura da Terra. Dessa maneira, a ISS decai continuamente, mas nunca se aproxima ou se afasta da superfície do planeta. Nesse sentido, digo que é uma queda sem fim, isto é, uma queda que nunca acontece. Essa boa idéia, infelizmente, não é minha. Obrigado por isso: é Sir I. Newton!
A órbita é uma queda infinitamente livre (I. Newton)
Newton argumentou que se você atirar um rifle horizontalmente do topo de uma montanha e com a velocidade crescente do projétil, o projétil cairá cada vez mais longe do local de lançamento. Portanto, deve haver um valor de velocidade tal que o projétil não caia mais, mas orbite a Terra. Esse experimento mental de Newton é conhecido na literatura científica como canhão de Newton (ou canhão de Newton). Ilustração abaixo, obtida por este aplicativo na linha (tente e divirta-se escolhendo a velocidade inicial do canhão disparado em m / s!), ilustra a ideia de várias trajetórias de projéteis lançadas horizontalmente do topo de uma montanha.

Imprima uma tela de aplicativo que simula o canhão de Newton. (Fonte)
Nestes outros conexão você pode encontrar uma versão visualmente mais moderna e ainda mais completa do canhão de Newton. Se você pesquisar no Google, encontrará inúmeras outras versões. Gosto deste simulador que publiquei impresso, porque mostra a figura original apresentada no trabalho de Newton.
Mas devo observar que há uma diferença sutil entre um elevador caindo perto da Terra e a ISS em sua queda infinita. Lá, a uma altitude de h = 400 km, onde está o ISS, a queda não ocorre em 9,8 m / s², mas em 8,7 m / s², como calculamos acima. Mas é uma queda, e com razão com a gravidade. E por essa mesma razão, a sensação de estar em órbita é a mesma que sem peso e “flutuando”, uma sensação análoga a estar em um elevador em queda livre.
A NASA chamou essa situação de gravidade zero. E isso criou muita confusão na mente das pessoas que entenderam a idéia literalmente, acreditando que a gravidade no espaço é realmente zero. Ultimamente, chama-se microgravidade, o que também não explica muito, mas alerta que os astronautas têm uma sensação de gravidade muito fraca, “micro”, quase zero. Mas é apenas e apenas um sentimento, um efeito colateral de queda sem fim.
O nome correto para essa situação é ausência de peso. Palavrão a dizer que se dentro de um elevador em queda houvesse uma balança ou ISS orbitando a Terra com um corpo em sua placa, porque tanto a balança quanto o corpo cairiam e com a mesma aceleração de = g naquele ponto, a balança indicaria zero. Nesse caso, seria impossível pesar (medir) o peso corporal usando uma balança, daí o termo ausência de peso.
O nome científico para a sensação de gravidade zero é leve!
Abraço do prof. Dulcidio! E física em uma veia!
De fato, haverá atração mútua entre os corpos, porque, de acordo com a terceira lei de Newton, se o corpo A atrai outro corpo B, B também atrai A pela força da mesma natureza, com a mesma intensidade, na mesma direção, mas em direções opostas.
² Duas observações são necessárias aqui: (A) Na figura, a ISS parece orbitar a Terra em um plano contendo os pólos da Terra. Mas isso é apenas uma breve visão geral da ideia. A órbita da ISS está inclinada a 51,6 graus do equador da Terra e não cruza os pilares da Terra; (B) A ISS é aproximadamente do tamanho de um campo de futebol (contando painéis solares). Portanto, na escala da ilustração, isso seria apenas um pequeno ponto de tamanho insignificante.
Jpublicado na revista Physics in vein!